Show Navigation
|
Hide Navigation
How Hillshade works |
|
|
Release 9.2
Last modified January 3, 2008 |
|
The Hillshade function obtains the hypothetical illumination of a surface by determining illumination values for each cell in a raster. It does this by setting a position for a hypothetical light source and calculating the illumination values of each cell in relation to neighboring cells. It can greatly enhance the visualization of a surface for analysis or graphical display, especially when using transparency.
The Hillshade algorithm
To calculate the shade value, first the altitude and azimuth of the illumination source is needed. These values will be processed along with calculations for slope and aspect to determine the final hillshade value for each cell in the output raster.
The algorithm for calculating the Hillshade value is:
(1) Hillshade = 255.0 * ( ( cos(Zenith_rad) * cos(Slope_rad) ) + ( sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad) ) )
Note that if the calculation of Hillshade value is < 0, the cell value will be = 0.
Computing the illumination angle
The altitude of the illumination source is specified in degrees above horizontal. However, the formula for calculating the Hillshade value requires the angle be represented in radians, and be the deflection from the vertical. The direction straight up from the surface (directly overhead) is labelled the 'Zenith'. The zenith angle is measured from the zenith point to the direction of the illumination source, and is the 90° complement to the altitude. To calculate the illumination angle, the first step is to convert the altitude angle to the zenith angle. The second step is to convert the angle to radians.
Changing altitude to zenith angle:
(2) Zenith_deg = 90 - Altitude
Convert to radians:
(3) Zenith_rad = Zenith */ 180.0
Computing the illumination direction
The direction of the illumination source, azimuth, is specified in degrees. The Hillshade formula requires this angle to be in units of radians. First, the azimuth angle is changed from its geographic unit (compass direction) to an mathematic unit (right angle). Next, the azimuth angle is converted to radians Change azimuth angle measure:
(4) Azimuth_math = 360.0 - Azimuth + 90
Note that if Azimuth_math >= 360.0, then:
(5) Azimuth_math = Azimuth_math - 360.0
Convert to radians:
(6) Azimuth_rad = Azimuth_math *
Computing Slope and Aspect
A moving 3 x 3 window visits each cell in the input raster and for each cell in the center of the window, an aspect and slope value is calculated using an algorithm that incorporates the values of the cell's eight neighbors. The cells are identified as letters 'a' to 'i', with 'e' representing the cell for which the aspect is being calculated.
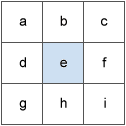
The rate of change in the x direction for cell 'e' is calculated with the following algorithm:
(7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * cellsize)
The rate of change in the y direction for cell 'e' is calculated with the following algorithm:
(8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * cellsize)
The steepest downhill descent from each cell in the surface is the slope. The algorithm for calculating the slope in radians, incorporating the z-factor, is:
(9) Slope_rad = ATAN ( z_factor * √ ( [dz/dx]2 + [dz/dy]2) )
The direction the steepest downslope direction is facing is the aspect. Aspect in radians is defined in the range of 0 to 2
, with 0 toward east. The aspect is determined under the rules in the following algorithm: (10)
if [dz/dx] is non-zero: Aspect_rad = atan2 ([dz/dy], -[dz/dx]) if Aspect_rad < 0 then Aspect_rad = 2
if [dz/dx] is zero if [dz/dy] > 0 then Aspect_rad =
Reference
Burrough, P. A. and McDonell, R.A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), p. 190.A Hillshade calculation example
As an example, the hillshade value of the center cell of the moving window will be calculated.
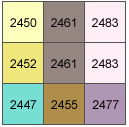
The cell size is 5 units. The default Altitude of 45 degrees and Azimuth of 315 degrees will be used.
- Illumination angle
The calculation for Zenith angle from equation 2 is:
(2) Zenith_deg = 90 - Altitude = 90 - 45 = 45
And converted to radians from equation 3 is:
(3) Zenith_rad = Zenith_deg *
- The illumination direction
The calculation for converting the azimuth angle from geographic to mathematic angle with equation 4 is:
(4) Azimuth_math = 360.0 - Azimuth + 90 = 360.0 - 315 + 90 = 135
Converting azimuth angle to radians with equation 6 is:
(6) Azimuth_rad = Azimuth_math *
- Slope and Aspect
The calculation for the rate of change in the x direction for center cell 'e' is:
(7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * cellsize) = ((2483+ 4966 + 2477) - (2450 + 4904 + 2447)) / (8 * 5) = (9926 - 9801)/ 40 = 3.125
The calculation for rate of change in the y direction for center cell 'e' is:
(8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * cellsize) = (2447 + 4910 + 2477) - (2450 + 4922 + 2483) / (8 * 5) = (9834 - 9855) / 40 = -0.525
The calculation for the Slope angle is:
(9) Slope_rad = ATAN ( z_factor * √ ( [dz/dx]2 + [dz/dy]2) ) = atan(1 * sqrt(3.125 * 3.125 + -0.525 * -0.525)) = 1.26511
The calculation for the Aspect_rad angle from rule 10 is: (since dz/dx is non-zero in this example)
Aspect_rad = atan2 ([dz/dy], -[dz/dx]) = atan2(-0.525, -3.125) = -2.9751469600412
(and since this value is less than 0, this part of the rule applies):
Aspect_rad = 2
- Hillshade
The final calculation for the Hillshade is:
Hillshade = 255.0 * ( ( cos(Zenith_rad) * cos(Slope_rad) ) + ( sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad) ) ) = 255.0 * ( ( cos(0.7857142857) * cos(1.26511) ) + ( sin(0.7857142857) * sin(1.26511) * cos(2.3571428571 - 3.310567) ) ) = 153.82
Since the output raster is of integer type, the Shade value for center cell 'e' = 154.