Show Navigation
|
Hide Navigation
How Slope works |
|
|
Release 9.2
Last modified January 3, 2008 |
|
For each cell, Slope calculates the maximum rate of change in value from that cell to its neighbors. Basically, the maximum change in elevation over the distance between the cell and its eight neighbors identifies the steepest downhill descent from the cell.
Conceptually, the Slope function fits a plane to the z-values of a 3 x 3 cell neighborhood around the processing or center cell. The slope value of this plane is calculated using the average maximum technique (see References). The direction the plane faces is the aspect for the processing cell.
The lower the slope value, the flatter the terrain; the higher the slope value, the steeper the terrain.
If there is a cell location in the neighborhood with a NoData z-value, the z-value of the center cell will be assigned to the location. At the edge of the raster, at least three cells (outside the raster's extent) will contain NoData as their z-values. These cells will be assigned the center cell's z-value. The result is a flattening of the 3 x 3 plane fitted to these edge cells, which usually leads to a reduction in the slope.
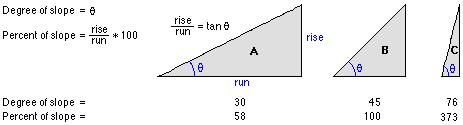
The output slope raster can be calculated in two types of units, degrees or percent (called 'percent rise').
The percent rise can be better understood if you consider it as the rise divided by the run, multiplied by 100. Consider triangle B below. When the angle is 45 degrees, the rise is equal to the run, and the percent rise is 100 percent. As the slope angle approaches vertical (90 degrees), as in triangle C, the percent rise begins to approach infinity.
The Slope algorithm
The rate of change (delta) of the surface in the horizontal (dz/dx) and vertical (dz/dy) directions from the center cell determines the slope. The basic algorithm used to calculate the slope is:
slope_radians = ATAN ( √ ( [dz/dx]2 + [dz/dy]2 ) )
Slope is commonly measured in degrees, which uses the algorithm:
slope_degrees = ATAN ( √ ( [dz/dx]2 + [dz/dy]2 ) ) * 57.29578
The slope algorithm can also be interpreted as:
slope_degrees = ATAN (rise_run) * 57.29578
where: rise_run = √ ( [dz/dx]2 + [dz/dy]2 ]
The values of the center cell and its eight neighbors determine the horizontal and vertical deltas. The neighbors are identified as letters from 'a' to 'i', with 'e' representing the cell for which the aspect is being calculated.
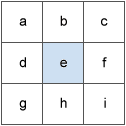
The rate of change in the x direction for cell 'e' is calculated with the algorithm:
[dz/dx] = ((c + 2f + i) - (a + 2d + g) / (8 * x_cell_size)
The rate of change in the y direction for cell 'e' is calculated with the following algorithm:
[dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * y_cell_size)
References
Burrough, P. A. and McDonell, R.A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), p. 190.A Slope calculation example
As an example, the slope value of the center cell of the moving window will be calculated.
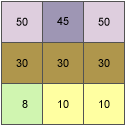
The cell size is 5 units. The default slope measure of degrees will be used.
The rate of change in the x direction for the center cell 'e' is:
[dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * x_cell_size) = ((50 + 60 + 10) - (50 + 60 + 8)) / (8 * 5) = (120 - 118) / 40 = 0.05
The rate of change in the y direction for cell 'e' is:
[dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * y_cell_size) = ((8 + 20 + 10) - (50 + 90 + 50)) / (8 * 5) = (38 - 190 ) / 40 = -3.8
Taking the rate of change in the x and y direction, the slope for the center cell 'e' is calculated using:
rise_run = √ ( [dz/dx]2 + [dz/dy]2 ) = √ ( (0.05)2 + (-3.8)2 ] = √ [ 0.0025 + 14.44 ] = 3.80032
slope_degrees = ATAN (rise_run) * 57.29578 = ATAN (3.80032) * 57.29578 = 1.31349 * 57.29578 = 75.25762
The integer slope value for cell 'e' is 75 degrees.
