Extensions > 3D Analyst > 3D surfaces
About 3D surfaces |
|
|
Release 9.2
Last modified February 29, 2008 |
Print all topics in : "3D surfaces" |
A 3D surface model is a digital representation of features, either real or hypothetical, in three-dimensional space. Some simple examples of 3D surfaces are a landscape, an urban corridor, gas deposits under the earth, or a network of well depths to determine water table depth. These are all examples of real features, but they could be derived or imaginary. An example of a derived surface is the contaminant levels of a particular bacteria in each well. Those contaminants could be mapped as a 3D surface too. Imaginary examples of 3D surfaces are often the types found in video games or computer simulation environments.
A 3D surface is usually derived, or calculated, using specially designed algorithms that sample point, line or polygon data and convert them into a digital 3D surface. ArcGIS can create and store three types of surface model: raster, TIN, and Terrain.
Below are examples of raster, TIN, and Terrain surfaces, side by side.

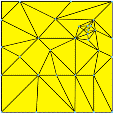
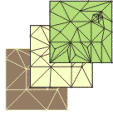
These three types of surface models can be created from a variety of data sources. The two main methods of creating surface models are interpolation and triangulation. There are several interpolation methods, such as Inverse Distance Weighted, Spline, Kriging, and Natural Neighbors. You can build triangulated surfaces by creating a TIN or by adding elements to an existing TIN. You can also convert between Terrain, TIN, and raster surface models.
Raster, TIN and Terrain surfaces are all types of a functional surface. A functional surface is a continuous field of values that may vary over an infinite number of points. For example, points in an area on the earth's surface may vary in elevation, proximity to a feature, or concentration of a particular chemical. Any of these values may be represented on the z-axis in a three-dimensional x,y,z coordinate system, so they are often called z-values.
Surface models allow you to store surface information in a GIS. Because a surface contains an infinite number of points, it is impossible to measure and record the z-value at every point. A surface model approximates a surface by taking a sample of the values at different points on the surface and interpolating the values between these points.
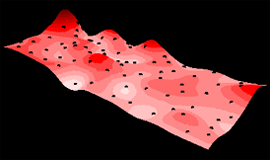
The illustration below shows a surface model of chemical concentration across an area. Points show where the concentration was sampled.
Raster surfaces
GIS data can generally be categorized into two major types: raster and vector. Vector data is defined by arcs, nodes, lines, and their associated relationships that comprise geospatial data. Real-world features, and surfaces, can be represented as vector data stored in a GIS. Raster data is a rectangular array of a matrix of cells, represented in rows and columns. Each cell represents a defined square area on the earth's surface and holds a value that is static across the entire cell. A surface can be represented as raster data where each cell in the data represents some value of real-world information. It could be elevation data, contamination concentrations, water table levels, and so on.
Learn more about raster data
Raster data can be further subdivided into categories, such as thematic, pictures, or continuous data. Surfaces represented as raster data are a form of continuous data. Continuous data is also referred to as field, nondiscrete, or surface data. A continuous surface represents phenomena in which each location on the surface is a measure of the concentration level or its relationship from a fixed point in space or from an emitting source.
Elevation models are one such example of raster surface models. The fixed point may be a spot height derived from photogrammetric methods, but interpolation between heights help form the digital elevation model (DEM). Since raster surfaces are usually stored in grid format with uniformly spaced cells, the smaller the cells, the greater the locational precision of the grid. The example below compares a higher precision grid (left) to a lower precision grid (right).


The locational precision of individual features—for example, the summit of a mountain—is directly related to the size of the grid cells. In the example above, a very coarse elevation surface data is depicted as a surface model in a two-dimensional, planar view. Raster surfaces can be generated and modeled with other image sources for 3D perspective views as well, such as this high resolution DEM with hillshade (below).

TIN surfaces
Triangular Irregular Networks (TINs) have been used by the GIS community for many years and are a digital means to represent surface morphology. TINs are a form of vector based digital geographic data and are constructed by triangulating a set of vertices (points). The vertices are connected with a series of edges to form a network of triangles. There are different methods of interpolation to form these triangles, such as Delaunay triangulation or distance ordering. ArcGIS supports the Delaunay triangulation method.
The resulting triangulation satisfies the Delaunay triangle criterion, which ensures that no vertex lies within the interior of any of the circumcircles of the triangles in the network. If the Delaunay criterion is satisfied everywhere on the TIN, the minimum interior angle of all triangles is maximized. The result is that long, thin triangles are avoided as much as possible.
The edges of TINs form contiguous, nonoverlapping triangular facets and can be used to capture the position of linear features that play an important role in a surface, such as ridgelines or stream courses. The graphics below show the nodes and edges of a TIN (left) and the nodes, edges, and faces of a TIN (right).
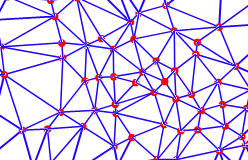
Because nodes can be placed irregularly over a surface, TINs can have a higher resolution in areas where a surface is highly variable or where more detail is desired and a lower resolution in areas that are less variable.
The input features used to create a TIN remain in the same position as the nodes or edges in the TIN. This allows a TIN to preserve all the precision of the input data while simultaneously modeling the values between known points. You can include precisely located features on a surface—such as mountain peaks, roads, and streams—by using them as input features to the TIN nodes.
TIN models are less widely available than raster surface models and tend to be more time consuming to build and process. The cost of obtaining good source data can be high, and processing TINs tends to be less efficient than processing raster data because of the complex data structure.
TINs are typically used for high-precision modeling of smaller areas, such as in engineering applications, where they are useful because they allow calculations of planimetric area, surface area, and volume.
Learn more about TIN surfaces
Terrain surfaces
Representing elevation data as surfaces in ArcGIS has never been easier with the implementation of Terrain datasets in version 9.2. Remotely sensed elevation data, such as LIDAR and SONAR point measurements number in the hundreds of thousands to hundreds of millions. Managing and modeling this type of data is cumbersome for most hardware and software available today. The terrain dataset allows a series of rules and conditions to be generated that index source data into an ordered set of TIN pyramids that gets generated on the fly.
Rendering very large TINs is generally difficult, partially due to limitations by hardware such as video cards. However, terrains are beneficial in that you render the areas that you need to visualize at an optimized resolution. Thus, if you have a small scale area in ArcGlobe or ArcMap, fewer nodes will be utilized by the terrain to generate the TIN rendered on your screen. However, if you zoom into an area at large scale, a full resolution (utilizing all the nodes for that area) will be used to generate a TIN on the fly. The obvious advantage is that only a small portion of the study area is being rendered with large numbers of nodes, or a subsampled collection of nodes is used to generate a lower resolution TIN on the fly.
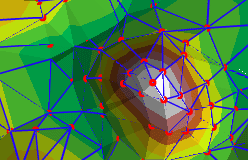
An example of this is shown in the following graphic.
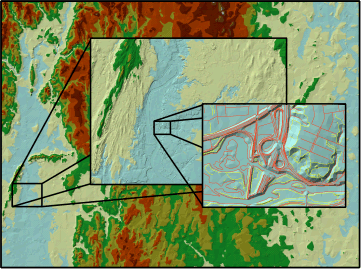
The graphic below illustrates how multiple types of feature classes can participate to generate TIN pyramids.
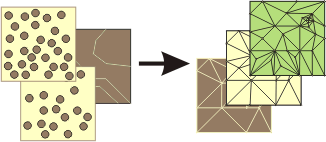
Learn more about Terrain surfaces