Extensions > Spatial Analyst > Analysis concepts > Distance analysis
Cost Distance algorithm |
|
|
Release 9.2
Last modified May 2, 2007 |
Print all topics in : "Distance analysis" |
The Cost functions are similar to Euclidean functions, but instead of calculating the actual distance from one point to another, the Cost functions determine the shortest weighted distance (or accumulated travel cost) from each cell to the nearest cell in the set of source cells. The weighted distance functions apply distance in cost units, not in geographic units.
All weighted-distance functions require a source raster and a cost raster. A source raster can contain single or multiple zones, which may or may not be connected. All cells that have a value (including zero) are processed as source cells. All nonsource cells must be assigned NoData in the source raster.
The Cost Distance function creates an output raster in which each cell is assigned the accumulative cost to the closest source cell. The algorithm utilizes the node/link cell representation. In the node/link representation, each center of a cell is considered a node and each node is connected to its adjacent nodes by links.
Every link has an impedance associated with it. The impedance is derived from the costs associated with the cells at each end of the link (from the cost surface) and from the direction of movement. The cost assigned to each cell represents the cost per unit distance for moving through the cell. Thus, each cell is multiplied by the cell resolution while also compensating for diagonal movement to obtain the total cost of passing through a cell. To calculate the cost to travel through each cell, the following formula is used:
costpercell = cost assigned to the cell * the cell resolution
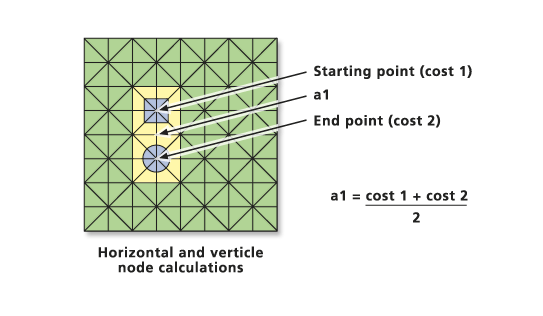
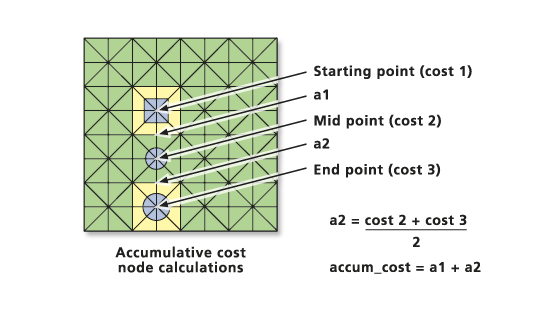
When moving from a cell to one of its four directly connected neighbors, the cost to move across the links to the neighboring node is one times cell 1, plus cell 2, divided by two.
a1 = (cost1 + cost2) / 2
where cost1 is the cost of cell 1, cost2 is the cost of cell 2, and a1 is the total cost of the link from cell 1 to cell 2.
The accumulative cost is determined by the following formula:
accum_cost = a1 + (cost2 + cost3) / 2
where cost2 is the cost of cell 2, cost3 is the cost of cell 3, and accum_cost is the accumulative cost to move into cell 3 from cell 1. a2 is the cost of moving from cell 2 to 3.
If the movement is diagonal, the cost to travel over the link is 1.414214 (or the square root of two) times the cost of cell 1 plus the cost of cell 2, divided by two.
a1 = 1.414214 (cost1 + cost2) / 2
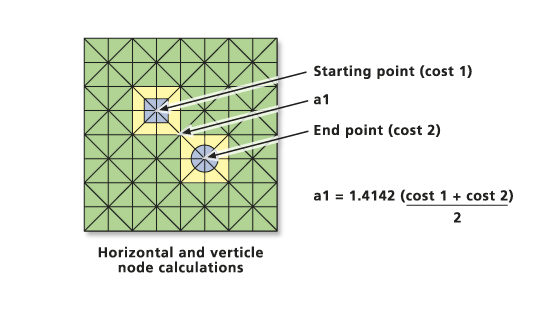
When determining the accumulative cost for diagonal movement, the following formula must be used:
accum_cost = a1 + 1.414214(cost2 + cost3) / 2
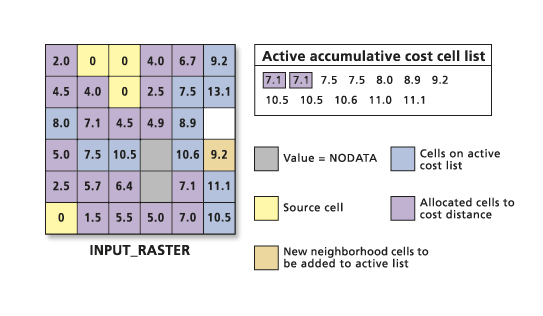
Creating an accumulative cost-distance raster using graph theory can be viewed as an attempt to identify the lowest cost cell and add it to an output list. It is an iterative process that begins with the source cells. The goal of each cell is to be assigned quickly to the output cost-distance raster.
In the first iteration, the source cells are identified and assigned to zero since there is no accumulative cost to return to themselves. Next, all the source cell's neighbors are activated, and a cost is assigned to the links between the source cell nodes and the neighborhood cells' nodes using the above accumulative cost formulas. Each of these neighborhood cells can reach a source; consequently, they can be chosen or assigned to the output accumulative cost raster. To be assigned to the output raster, a cell must have the next least-cost path to a source.
The accumulative cost values are arranged in a list from the lowest accumulative cost to the highest.
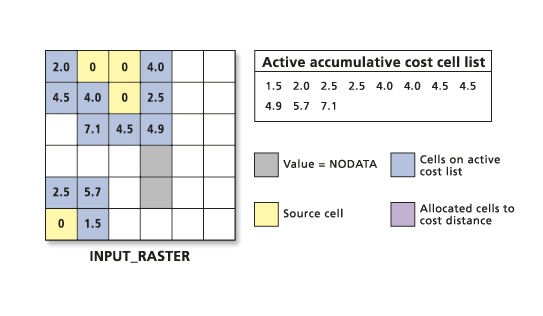
The lowest cost cell is chosen from the active accumulative cost cell list, and the value for that cell location is assigned to the output cost-distance raster. The list of active cells expands to include the neighbors of the chosen cell, because those cells now have a way to reach a source. Only those cells that can possibly reach a source can be active in the list. The cost to move into these cells is calculated using the accumulative cost formulas.
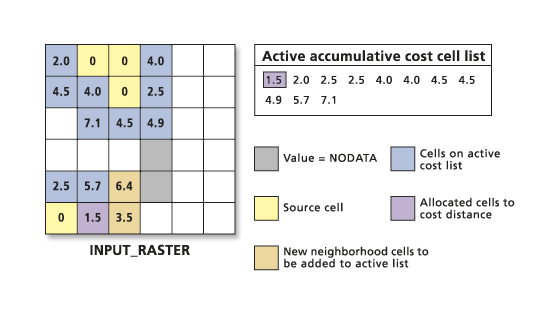
Again, the active cell on the list with the lowest cost is chosen, the neighborhood is expanded, the new costs are calculated, and the new cost cells are added to the active list.
Source cells do not have to be connected. All disconnected sources contribute equally to the active list. Only the cell with the lowest accumulative cost is chosen and expanded, regardless of the source to which it will be allocated.
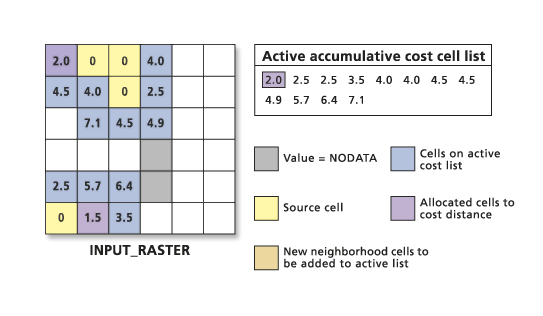
This allocation process continues. Furthermore, cells on the active list are updated if a new, cheaper route is created by the addition of new cell locations to the output raster.
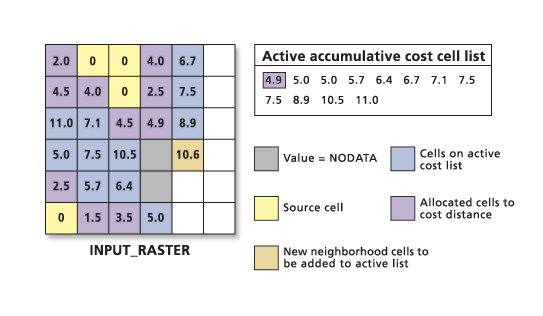
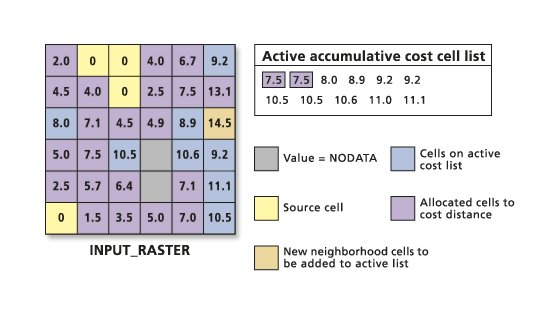
This updating can occur with the advent of new paths for cells on the active list as more cells are allocated to the output raster. When the cell with the lowest value on the active accumulative cost list is allocated to the output raster, all the accumulative costs are calculated. These costs are also calculated for the neighboring cells of the newly assigned output cell, even if the neighboring cells are on the active list through another cell. If the new accumulative cost for the locations on the active list is greater than the one the cells currently have, the value is ignored. If the accumulative cost is less, the old accumulative cost for the location is replaced on the active list with the new value. That cell, which has discovered a cheaper and more desirable path to a source, moves up the active chosen list. In the example below, the cell location at row 3, column 1 (highlighted by the box), had an accumulative cost of 11.0 when it was put on the active list to reach the source at the top of the raster. However, because the lower source expanded to this location, the cell had access to a cheaper accumulative cost path to reach a source. The value for the location was updated on the active list and allocated to the output earlier because of this lower accumulative cost.
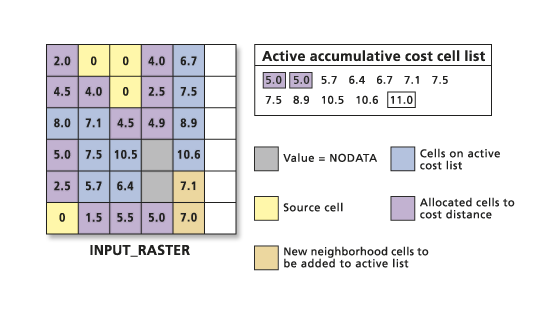
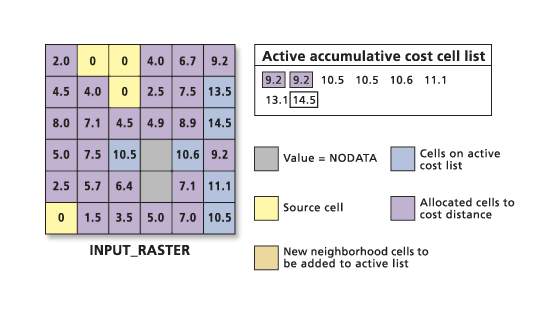
If there are multiple zones or disconnected sets of source cells on the input source raster, the growing process continues and allocates the cheapest cost cell from the active list regardless of which source it is from. When the growth fronts meet, the least-cost path back to the source proceeds until all eligible cells have received a cost value.
It is conceivable that when the growing patterns meet, cells from one growth pattern will discover they can reach a source cell in another set or growth pattern more cheaply; if so, they will be reassigned to the new source. This behavior was witnessed by the cell at row 3, column 1, earlier but is also exemplified below by the cell located at row 3, column 6.
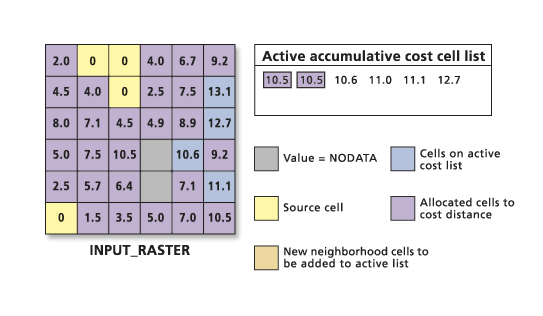
When all cells have been chosen from the active list, the result is the accumulative cost or weighted-distance raster. The procedure used ensures that the lowest accumulative cost is guaranteed for each cell. This process continues for all cells until the edge of the raster is encountered, the boundary of the window is found, or the maximum distance is reached.
No travel is allowed through cells containing NoData values. The least accumulative cost for cells on the back side of a group of NoData cells is determined by the cost to travel around these locations. If a cell location is assigned NoData on the input cost raster, then NoData will be assigned to the cell location on the cost distance output raster.
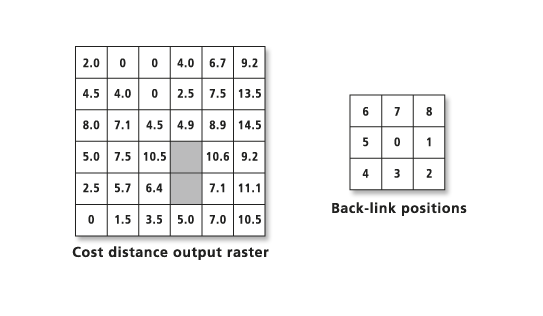
The cost distance raster identifies the accumulative cost for each cell to return to the closest cell in the set of source cells. It does not show which source cell to return to or how to get there. The cost back link returns a raster with a value range from 0 to 8 that can be used to reconstruct the route to the source. Each value of 0 through 8 identifies the neighboring cell to move into to get back to the source.
If the cell is assigned five as part of the least-cost path to a source, the path should move to the neighboring cell on the left. If that cell has seven, the path should move due north.
Cost allocation produces a raster similar to the Euclidean allocation function; like the Euclidean function, the raster identifies which cells will be allocated to which source. Unlike the Euclidean function, however, it does so on the basis of the lowest accumulative cost to reach a source.
Once the accumulative cost and back link rasters are created, least-cost path routes can be derived from any designated destination cell or zones. The Cost Path function retraces the destination cells through the back link raster to a source.
Learn more about least-cost path and least-cost corridor