Map projections and coordinate systems > Geographic coordinate systems
Spheroids and spheres |
|
|
Release 9.2
Last modified November 9, 2006 |
Print all topics in : "Geographic coordinate systems" |
The shape and size of a geographic coordinate system's surface is defined by a sphere or spheroid. Although the earth is best represented by a spheroid, the earth is sometimes treated as a sphere to make mathematical calculations easier. The assumption that the earth is a sphere is possible for small-scale maps (smaller than 1:5,000,000). At this scale, the difference between a sphere and a spheroid is not detectable on a map. However, to maintain accuracy for larger-scale maps (scales of 1:1,000,000 or larger), a spheroid is necessary to represent the shape of the earth. Between those scales, choosing to use a sphere or spheroid will depend on the map's purpose and the accuracy of the data.
Definition of a spheroid
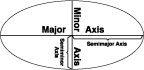
A sphere is based on a circle, while a spheroid (or ellipsoid) is based on an ellipse.
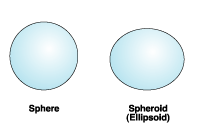
The shape of an ellipse is defined by two radii. The longer radius is called the semimajor axis, and the shorter radius is called the semiminor axis.
Rotating the ellipse around the semiminor axis creates a spheroid. A spheroid is also known as an oblate ellipsoid of revolution. The following graphic shows the semimajor and semiminor axes of a spheroid.
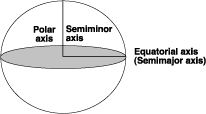
A spheroid is defined by either the semimajor axis, a, and the semiminor axis, b, or by a and the flattening. The flattening is the difference in length between the two axes expressed as a fraction or a decimal. The flattening, f, is:
f = (a - b) / a
The flattening is a small value, so usually the quantity 1/f is used instead. The spheroid parameters for the World Geodetic System of 1984 (WGS 1984 or WGS84) are:
a = 6378137.0 meters
b = 6356752.31424 meters
1/f = 298.257223563
The flattening ranges from zero to one. A flattening value of zero means the two axes are equal, resulting in a sphere. The flattening of the earth is approximately 0.003353. Another quantity that, like the flattening, describes the shape of a spheroid is the square of the eccentricity, e2. It is represented by:
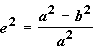
Defining different spheroids for accurate mapping
The earth has been surveyed many times to better understand its surface features and their peculiar irregularities. The surveys have resulted in many spheroids that represent the earth. Generally, a spheroid is chosen to fit one country or a particular area. A spheroid that best fits one region is not necessarily the same one that fits another region. Until recently, North American data used a spheroid determined by Clarke in 1866. The semimajor axis of the Clarke 1866 spheroid is 6,378,206.4 meters, and the semiminor axis is 6,356,583.8 meters.
Because of gravitational and surface feature variations, the earth is neither a perfect sphere nor a perfect spheroid. Satellite technology has revealed several elliptical deviations; for example, the South Pole is closer to the equator than the North Pole. Satellite-determined spheroids are replacing the older ground-measured spheroids. For example, the new standard spheroid for North America is the Geodetic Reference System of 1980 (GRS 1980), whose radii are 6,378,137.0 and 6,356,752.31414 meters. The GRS 1980 spheroid parameters were set by the International Union for Geodesy and Geophysics in 1979.
Because changing a coordinate system's spheroid will change all feature coordinate values, many organizations haven't switched to newer (and more accurate) spheroids.