Map projections and coordinate systems > Projected coordinate systems
About map projections |
|
|
Release 9.2
Last modified November 9, 2006 |
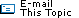
Print all topics in : "Projected coordinate systems" |
Whether you treat the earth as a sphere or a spheroid, you must transform its three-dimensional surface to create a flat map sheet. This mathematical transformation is commonly referred to as a map projection. One easy way to understand how map projections alter spatial properties is to visualize shining a light through the earth onto a surface, called the projection surface. Imagine the earth's surface is clear with the graticule drawn on it. Wrap a piece of paper around the earth. A light at the center of the earth will cast the shadows of the graticule onto the piece of paper. You can now unwrap the paper and lay it flat. The shape of the graticule on the flat paper is different from that on the earth. The map projection has distorted the graticule.
A spheroid can't be flattened to a plane any more easily than a piece of orange peel can be flattened—it will rip. Representing the earth's surface in two dimensions causes distortion in the shape, area, distance, or direction of the data.
A map projection uses mathematical formulas to relate spherical coordinates on the globe to flat, planar coordinates.
Different projections cause different types of distortions. Some projections are designed to minimize the distortion of one or two of the data's characteristics. A projection could maintain the area of a feature but alter its shape. In the graphic below, data near the poles is stretched.
The following diagram shows how three-dimensional features are compressed to fit onto a flat surface.
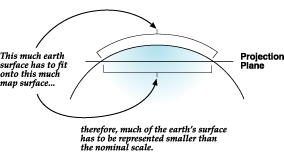
Map projections are designed for specific purposes. One map projection might be used for large-scale data in a limited area, while another is used for a small-scale map of the world. Map projections designed for small-scale data are usually based on spherical rather than spheroidal geographic coordinate systems.
Conformal projections
Conformal projections preserve local shape. To preserve individual angles describing the spatial relationships, a Conformal projection must show the perpendicular graticule lines intersecting at 90-degree angles on the map. A map projection accomplishes this by maintaining all angles. The drawback is that the area enclosed by a series of arcs may be greatly distorted in the process. No map projection can preserve shapes of larger regions.
Equal area projections
Equal area projections preserve the area of displayed features. To do this, the other properties—shape, angle, and scale—are distorted. In Equal area projections, the meridians and parallels may not intersect at right angles. In some instances, especially maps of smaller regions, shapes are not obviously distorted, and distinguishing an Equal area projection from a Conformal projection is difficult unless documented or measured.
Equidistant projections
Equidistant maps preserve the distances between certain points. Scale is not maintained correctly by any projection throughout an entire map. However, there are in most cases, one or more lines on a map along which scale is maintained correctly. Most Equidistant projections have one or more lines in which the length of the line on a map is the same length (at map scale) as the same line on the globe, regardless of whether it is a great or small circle, or straight or curved. Such distances are said to be true. For example, in the Sinusoidal projection, the equator and all parallels are their true lengths. In other Equidistant projections, the equator and all meridians are true. Still others (for example, Two-point Equidistant) show true scale between one or two points and every other point on the map. Keep in mind that no projection is equidistant to and from all points on a map.
Learn more about the Sinusoidal projection
Learn more about the Two-point Equidistant projection
True-direction projections
The shortest route between two points on a curved surface such as the earth is along the spherical equivalent of a straight line on a flat surface. That is the great circle on which the two points lie. True-direction, or Azimuthal projections maintain some of the great circle arcs, giving the directions or azimuths of all points on the map correctly with respect to the center. Some True-direction projections are also conformal, equal area, or equidistant.