Geoprocessing tool reference > Geostatistical Analyst toolbox
Understanding geostatistical analysis |
|
|
Release 9.3
Last modified October 28, 2008 |
Print all topics in : "Geostatistical Analyst toolbox" |
Generating a continuous surface used to represent a particular attribute is a key capability required in most geographic information system (GIS) applications. Perhaps the most commonly used surface type is a digital elevation model of terrain. These datasets are readily available at small scales for various parts of the world. However, just about any measurement taken at locations across a landscape, subsurface, or atmosphere can be used to generate a continuous surface. A major challenge facing most GIS modelers is to generate the most accurate surface possible from existing sample data as well as characterize the error and variability of the predicted surface. Newly generated surfaces are used in further GIS modeling and analysis as well as in 3D visualization. Understanding the quality of this data can greatly improve the utility and purpose of GIS modeling. This is the role of the Geostatistical Analyst toolbox.
Geostatistical Analyst uses sample points taken at different locations in a landscape and creates (interpolates) a continuous surface. The sample points are measurements of some phenomenon such as radiation leaking from a nuclear power plant, an oil spill, or elevation heights. Geostatistical Analyst derives a surface using the values from the measured locations to predict values for each location in the landscape.
Geostatistical Analyst provides two groups of interpolation techniques: deterministic and geostatistical. All methods rely on the similarity of nearby sample points to create the surface. Deterministic techniques use mathematical functions for interpolation. Geostatistics rely on both statistical and mathematical methods, which can be used to create surfaces and assess the uncertainty of the predictions.
In addition to providing various interpolation techniques, Geostatistical Analyst also provides many supporting tools. For example, prior to mapping, Exploratory Spatial Data Analysis (ESDA) tools can be used to assess the statistical properties of the data. Having explored the data, the user can then create a variety of output map types (for example, prediction, error of prediction, probability, and quantile) using many variants of kriging and cokriging algorithms (for example, ordinary, simple, universal, indicator, probability, and disjunctive) and associated tools (for example, data transformation, declustering, and detrending).
Understanding deterministic methods
Generally speaking, things that are closer together tend to be more alike than things that are farther apart. This is a fundamental geographic principle. Suppose you are a town planner and you need to build a scenic park in your town. You have several candidate sites, and you may want to model their viewsheds at each location. This will require a more detailed elevation surface dataset for your study area. Suppose you have preexisting elevation data for 1,000 locations throughout the town. You can use this to build a new elevation surface.
When trying to build the elevation surface, you can assume that the sample values closest to the prediction location will be similar. But how many sample locations should you consider? And should all the sample values be considered equally? As you move farther away from the prediction location, the influence of the points will decrease. Considering a point too far away may actually be detrimental because the point may be located in an area that is dramatically different from the prediction location.
One solution is to consider enough points to give a good prediction but few enough points to be practical. The number will vary with the amount and distribution of the sample points and the character of the surface. If the elevation samples are relatively evenly distributed, and the surface characteristics do not change significantly across your landscape, you can predict surface values from nearby points with reasonable accuracy. To account for the distance relationship, the values of closer points are usually weighted more heavily than those farther away.
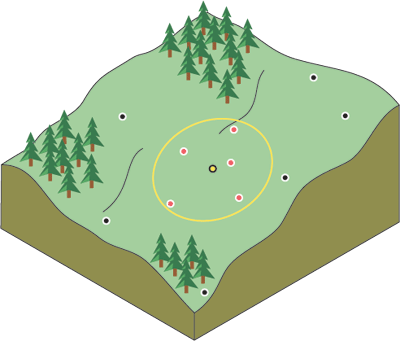
This is the basis for the Inverse Distance Weighted (IDW) interpolation technique. As its name implies, the weight of a value decreases as the distance increases from the prediction location.
A deterministic interpolation technique applies an established mathematical formula to the sample points. In the case of IDW, the formula is to multiply the values of the points that fall within a specified neighborhood from the processing cell by a weight that is derived from the distance the sample point is from the processing location.
The following are the deterministic methods available in Geostatistical Analyst:
- Inverse distance weighted
- Local polynomial
- Global polynomial
- Radial basis functions (RBS)
Global polynomial fits a polynomial formula to the sample points. Conceptually, global polynomial positions a plane between the sample points. The unknown height is then determined from the value on the plane that corresponds to the prediction location. The plane may be above certain points and below others. The goal for global polynomial is to minimize errors.
Local polynomial fits many smaller overlapping planes to the sample points, then uses the center of each plane as the prediction for each location in the study area.
Understanding geostatistical methods
A second family of interpolation methods consists of geostatistical methods that are based on statistical models that include autocorrelation (statistical relationships among the measured points). Not only do these techniques have the capability of producing prediction surfaces, but they can also provide some measure of the accuracy of these predictions.
Kriging is similar to Inverse Distance Weighted interpolation in that it weights the surrounding measured values to derive a prediction for each location. However, the weights are based not only on the distance between the measured points and the prediction location but also on the overall spatial arrangement among the measured points. To use the spatial arrangement in the weights, the spatial autocorrelation must be quantified.
Common steps in geostatistical data analysis
The following are the common steps in geostatistical data analysis:
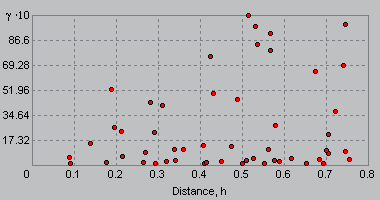
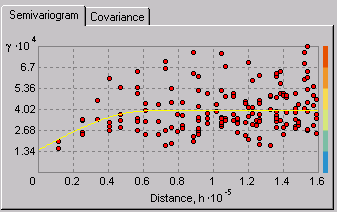
- Calculate the empirical semivariogram—Kriging, like most interpolation techniques, is built on the basic principle that things that are close to one another are more alike than those farther away (quantified here as spatial autocorrelation). The empirical semivariogram is a means to explore this relationship. Pairs that are close in distance should have a smaller difference than those farther away from one another. The extent to which this assumption is true can be examined in the empirical semivariogram.
- Fit a model—This is done by defining a model (the yellow line in the image below) that provides the best fit through the points. That is, you need to find a line such that the weighted squared difference between each point and the line is as small as possible. This is referred to as the weighted least-squares fit. This model quantifies the spatial autocorrelation in your data.
- Create the matrices—The equations for kriging are contained in matrices and vectors that depend on the spatial autocorrelation among the measured sample locations and prediction location. The autocorrelation values come from the semivariogram model. The matrices and vectors determine the kriging weights that are assigned to each measured value in the searching neighborhood.
- Make a prediction—From the kriging weights for the measured values, you can calculate a prediction for the location with the unknown value.