Show Navigation
|
Hide Navigation
You are here:
Geoprocessing tool reference > Spatial Statistics toolbox > Modeling Spatial Relationships toolset
Geoprocessing tool reference > Spatial Statistics toolbox > Modeling Spatial Relationships toolset
Regression analysis basics |
|
|
Release 9.3
Last modified April 24, 2009 |
Print all topics in : "Modeling Spatial Relationships toolset" |
Related Topics
Note:
This topic was updated for 9.3.1.
The spatial statistics toolbox provides effective tools for quantifying spatial patterns. Using the Hot Spot Analysis tool, for example, you can ask questions like:
- Are there places in the United States where people are persistently dying young?
- Where are the hot spots for crime, 911 emergency calls (see graphic below), or fires?
- Where do we find a higher than expected proportion of traffic accidents in a city?
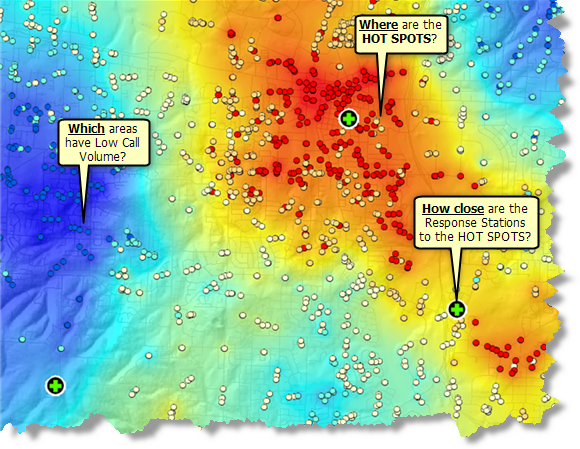
Analysis of 911 Emergency Call Data showing Call Hot Spots (Red), Call Cold Spots (Blue), and Locations of the Fire/Police Units Responsible for Responding (Green Crosses)
Each of the questions above asks "where?". The next logical question for the types of analyses above involves "why?":
- Why are there places in the United States where people persistently die young? What might be causing this?
- Can we model the characteristics of places that experience lots of crime, 911 calls, or fire events in order to help reduce these incidents?
- What are the factors contributing to higher than expected traffic accidents? Are there policy implications or mitigating actions that might reduce traffic accidents across the city and/or in particular high accident areas?
Regression Analysis
Regression analysis allows you to model, examine, and explore spatial relationships, and can help explain the factors behind observed spatial patterns. Regression analysis is also used for prediction. You may want to understand why people are persistently dying young in certain regions, for example, or may want to predict rainfall where there are no rain gauges.
OLS is the best known of all regression techniques. It is also the proper starting point for all spatial regression analyses. It provides a global model of the variable or process you are trying to understand or predict (early death/rainfall); it creates a single regression equation to represent that process. Geographically Weighted Regression (GWR) is one of several spatial regression techniques, increasingly used in geography and other disciplines. GWR provides a local model of the variable or process you are trying to understand/predict by fitting a regression equation to every feature in the dataset. When used properly, these methods are powerful and reliable statistics for examining/estimating linear relationships.
Linear relationships are either positive or negative. If you find that the number of search and rescue events increases when daytime temperatures rise, the relationship is said to be positive; there is a positive correlation. Another way to express this positive relationship is to say that search and rescue events decrease as daytime temperatures decrease. Conversely, if you find that the number of crimes goes down as the number of police officers patrolling an area goes up, the relationship is said to be negative. You can also express this negative relationship by stating that the number of crimes increases as the number of patrolling officers decreases. The graphic below depicts both positive and negative relationships, as well as the case where there is no relationship between two variables:
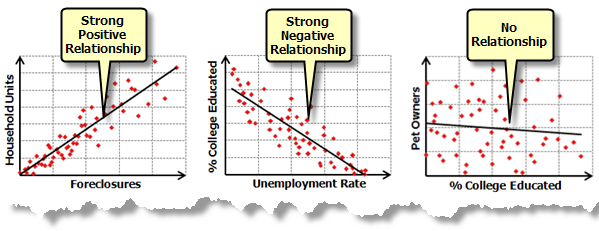
Positive and Negative Relationships as well as the case where two variables exhibit no relationship.
Correlation analyses and their associated graphics depicted above, test the strength of the relationship between two variables. Regression analyses, on the other hand, make a stronger claim; they attempt to demonstrate the degree to which one or more variables potentially promote positive or negative change in another variable.
Using Regression Analysis
Regression analysis can be used for a large variety of applications:
- Modeling fire frequency to determine high risk areas and to understand the factors that contribute to high risk areas.
- Modeling property loss from fire as a function of variables such as degree of fire department involvement, response time, property value, etc. If you find that response time is the key factor, you may need to build more fire stations. If you find that involvement is the key factor, you may need to increase equipment/officers dispatched.
- Modeling traffic accidents as a function of speed, road conditions, weather, etc. in order to inform policy aimed at decreasing accidents.
There are three primary reasons you might want to use regression analysis:
- To model some phenomena in order to better understand it and possibly use that understanding to affect policy or to make decisions about appropriate actions to take. Basic objective: to measure the extent that changes in one or more variables jointly affect changes in another. Example: Understand the key characteristics of the habitat for some particular endangered species of bird (perhaps precipitation, food sources, vegetation, predators… ) to assist in designing legislation aimed at protecting that species.
- To model some phenomena in order to predict values for that phenomenon at other places or other times. Basic objective: to build a prediction model that is consistent and accurate. Example: where are real estate values likely to go up next year? Or: there are rain gauges at particular places and a set of variables that explain the observed precipitation values… how much rain falls in places where there are no gauges? (Regression may be used in cases where interpolation is not effective because of insufficient sampling: there are no gauges on peaks or in valleys, for example).
- You can also use regression analysis to test hypotheses. Suppose you are modeling residential crime in order to better understand it, and hopefully implement policy to prevent it. As you begin your analysis you probably have questions or hypotheses you want to test:
- "Broken Window Theory" indicates that defacement of public property (graffiti, damaged structures, etc.) invite other crimes. Will there be a positive relationship between vandalism incidents and residential burglary?
- Is there a relationship between illegal drug use and burglary (might drug addicts steal to support their habits)?
- Are burglars predatory? Might there be more incidents in residential neighborhoods with higher proportions of elderly or female headed households?
- Is a person at greater risk for burglary if they live in a rich or a poor neighborhood?
You can use regression analysis to test these relationships and answer your questions.
Regression Analysis components
It is impossible to discuss regression analysis without first becoming familiar with a few terms and basic concepts specific to regression statistics:
Regression equation: this is the mathematical formula applied to the explanatory variables in order to best predict the dependent variable you are trying to model. Unfortunately for those in the Geosciences who think of X and Y as coordinates, the notation in regression equations for the dependent variable is always "y" and for independent or explanatory variables is always "X". Each independent variable is associated with a regression coefficient describing the strength and the sign of that variable's relationship to the dependent variable. A regression equation might look like this (y is the dependent variable, the X's are the explanatory variables, and the β's are regression coefficients; each of these components of the regression equation are explained further below):
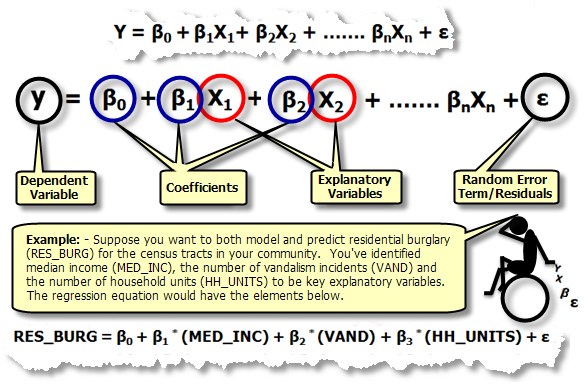
Elements of an OLS Regression Equation
-
Dependent variable (y): this is the variable representing the process you are trying to predict or understand (e.g., residential burglary, foreclosure, rainfall). In the regression equation, it appears on the left side of the equal sign. While you can use regression to predict the dependent variable, you always start with a set of known y values and use these to build (or to calibrate) the regression model. The known y values are often referred to as observed values.
-
Independent/Explanatory variables (X): these are the variables used to model or to predict the dependent variable values. In the regression equation, they appear on the right side of the equal sign and are often referred to as explanatory variables. We say that the dependent variable is a function of the explanatory variables. If you are interested in predicting annual purchases for a proposed store, you might include in your model explanatory variables representing the number of potential customers, distance to competition, store visibility, and local spending patterns, for example.
-
Regression coefficients (β): coefficients are computed by the regression tool. They are values, one for each explanatory variable, that represent the strength and type of relationship the explanatory variable has to the dependent variable. Suppose you are modeling fire frequency as a function of solar radiation, vegetation, precipitation and aspect. You might expect a positive relationship between fire frequency and solar radiation (the more sun, the more frequent the fire incidents). When the relationship is positive, the sign for the associated coefficient is also positive. You might expect a negative relationship between fire frequency and precipitation (places with more rain have fewer fires). Coefficients for negative relationships have negative signs. When the relationship is a strong one, the coefficient is large. Weak relationships are associated with coefficients near zero.
β
0 is the regression intercept. It represents the expected value for the dependent variable if all of the independent variables are zero.
P-Values: most regression methods perform a statistical test to compute a probability, called a p-value, for the coefficients associated with each independent variable. The null hypothesis for this statistical test states that a coefficient is not significantly different from zero (in other words, for all intents and purposes, the coefficient is zero and the associated explanatory variable is not helping your model). Small p-values reflect small probabilities, and suggest that the coefficient is, indeed, important to your model with a value that is significantly different from zero (the coefficient is NOT zero). You would say that a coefficient with a p value of 0.01, for example, is statistically significant at the 99% confidence level; the associated variable is an effective predictor. Variables with coefficients near zero do not help predict or model the dependent variable; they are almost always removed from the regression equation, unless there are strong theoretical reasons to keep them.
R 2 /R-Squared: Multiple R-Squared and Adjusted R-Squared are both statistics derived from the regression equation to quantify model performance. The value of R-squared ranges from 0 to 100 percent. If your model fits the observed dependent variable values perfectly, R-squared is 1.0 (and you, no doubt, have made an error… perhaps you've used a form of y to predict y). More likely, you will see R-squared values like 0.49, for example, which you can interpret by saying: this model explains 49% of the variation in the dependent variable. To understand what the R-squared value is getting at, create a bar graph showing both the estimated and observed Y values sorted by the estimated values. Notice how much overlap there is. This graphic provides a visual representation of how well the model's predicted values explain the variation in the observed dependent variable values. View an illustration. The Adjusted R-Squared value is always a bit lower than the Multiple R-Squared value because it reflects model complexity (the number of variables) as it relates to the data.
Residuals: these are the unexplained portion of the dependent variable, represented in the regression equation as the random error term, ε. View an illustration. Known values for the dependent variable are used to build and to calibrate the regression model. Using known values for the dependent variable (y) and known values for all of the explanatory variables (the Xs), the regression tool constructs an equation that will predict those known y values, as well as possible. The predicted values will rarely match the observed values exactly. The difference between the observed y values and the predicted y values are called the residuals. The magnitude of the residuals from a regression equation is one measure of model fit. Large residuals indicate poor model fit.
Building a regression model is an iterative process that involves finding effective independent variables to explain the process you are trying to model/understand, then running the regression tool to determine which variables are effective predictors… then removing/adding variables until you find the best model possible.
Regression Analysis Issues
OLS regression is a straightforward method, has well-developed theory behind it, and has a number of effective diagnostics to assist with interpretation and troubleshooting. OLS is only effective and reliable, however, if your data and regression model meet/satisfy all of the assumptions inherently required by this method (see the table below). Spatial data often violate the assumptions/requirements of OLS regression, and so it is important to use regression tools in conjunction with appropriate diagnostic tools that can assess whether or not regression is an appropriate method for your analysis, given the structure of the data and the model being implemented.
How Regression Models Go Bad. A serious violation for many regression models is misspecification. A misspecified model is one that is not complete - it is missing key/important explanatory variables and so it does not adequately represent what you are trying to model or trying to predict (the dependent variable, y); in other words, the regression model is not telling the whole story. Misspecification is evident whenever you see statistically significant spatial autocorrelation in regression residuals, or said another way: whenever you notice that the over and underpredictions (residuals) from your model tend to cluster spatially so that the over predictions cluster together in some portions of the study area and the underpredictions cluster together in others. Mapping regression residuals or the coefficients associated with Geographically Weighted Regression (GWR) analysis, will often provide clues about what you've missed. Running a Hot Spot Analysis on regression residuals may help reveal different spatial regimes that can be modeled in OLS with regional variables or can be remedied using the Geographically Weighted Regression (GWR) method. Suppose when you map your regression residuals you see that the model is always over predicting in the mountain areas and under predicting in the valleys - you will likely conclude that your model is missing an Elevation variable. There will be times, however, when the missing variable(s) are too complex to model, or impossible to quantify, or too difficult to measure. In these cases, you may be able to move to GWR or to another spatial regression method to get a well specified model.
The following table lists common problems with regression models, and the tools available in ArcGIS to help address them:
| Omitted explanatory variables (misspecification). | When key explanatory variables are missing from a regression model, coefficients and their associated p-values cannot be trusted. | Map and examine OLS residuals and GWR coefficients, or run Hot Spot Analysis on OLS regression residuals to see if this provides clues about possible missing variables. |
| Non-linear relationships. View an illustration. | OLS and GWR are both linear models. If the relationship between any of the explanatory variables and the dependent variable is non-linear, the resultant model will perform poorly. | Use the scatterplot matrix graphic to elucidate the relationships among all variables in the model. Pay careful attention to relationships involving the dependent variable. Curvilinearity can often be remedied by transforming the variables. View an illustration. Alternatively, use a non-linear regression method. |
| Data Outliers. View an illustration. | Influential outliers can pull modeled regression relationshsips away from their true best fit, biasing regression coefficients. | Use the scatterplot matrix and other graphing tools to examine extreme data values. Correct or remove outliers if they represent errors. When outliers are correct/valid values they cannot/should not be removed. Run the regression with and without the outliers to see how much they are effecting your results. |
| Non-stationarity. You might find that an INCOME variable, for example, has strong explanatory power in region A, but is insignificant or even switches signs in region B. View an illustration. | If relationships between your dependent and explanatory variables are inconsistent across your study area, computed standard errors will be artifically inflated. | The OLS tool in ArcGIS automatically tests for problems associated with non-stationarity (regional variation) and computes robust standard error values. View an illustration. When the probability associated with the Koenker test is small (< 0.05, for example), you have statistically significant non-stationarity and should consult the robust probabilities to determine if an explanatory variable is statistically significant or not. You will improve model results by using Geographically Weighted Regression. |
| Multicollinearity: one or a combination of explanatory variables is redundant. View an illustration. | Multicollinearity leads to an over-counting type of bias and an unstable/unreliable model. | The OLS tool in ArcGIS automatically checks for redundancy. Each explanatory variable is given a computed VIF value (variance inflation factor). When this value is large (> 7.5, for example), redundancy is a problem and the offending variables should be removed from the model or modified by creating an interaction variable or increasing the sample size. View an illustration. |
| Inconsistent variance in residuals. It may be that the model predicts well for small values of the dependent variable, but becomes unreliable for large values. View an illustration. | When the model predicts poorly for some range of values, results will be biased. | The OLS tool in ArcGIS automatically tests for inconsistent residual variance (called heteroskedasticity) and computes standard errors that are robust to this problem. When the probability associated with the Koenker test is small (< 0.05, for example), you should consult the robust probabilities to determine if an explanatory variable is statistically significant or not. View an illustration. |
| Spatially autocorrelated residuals. View an illustration. | When there is spatial clustering of the under/over predictions coming out of the model, it introduces an over-counting type of bias and renders the model unreliable. | Run the Spatial Autocorrelation tool on the residuals to ensure they do not exhibit statistically significant spatial clustering. Statistically significant spatial autocorrelation is often a symptom of misspecification (a key variable is missing from the model). View an illustration. |
| Normal distribution bias. View an illustration. | When the regression model residuals are not normally distributed with a mean of zero, the p-values associated with the coefficients are unreliable. | The OLS tool in ArcGIS automatically tests whether the residuals are normally distributed. When the Jarque-Bera statistic is significant (< 0.05, for example), your model is likely misspecified (a key variable is missing from the model). Examine the output residual map and perhaps GWR coefficient maps to see if this exercise reveals the key variables missing from the analysis. |
It is important to test for each of the problems listed above. Results can be 100% wrong (180 degrees different) if any of the problems above are ignored.
Spatial regression
Spatial data exhibit two properties that make it difficult (but not impossible) to meet the assumptions and requirements of traditional (non-spatial) statistical methods, like OLS regression:
- Geographic features are more often than not spatially autocorrelated; this means that features near each other tend to be more similar than features that are farther away. This creates an over-count type of bias for traditional (non-spatial) regression methods.
- Geography is important, and often the processes most important to the model are non-stationary; these processes behave differently in different parts of the study area. This characteristic of spatial data can be referred to as regional variation or spatial drift.
Spatial Autocorrelation. There seems to be a big difference between how a traditional statistician views spatial autocorrelation and how a spatial statistician views spatial autocorrelation. The traditional statistician sees it as a bad thing that needs to be removed from the data (through resampling, for example) because spatial autocorrelation violates underlying assumptions of many traditional (non-spatial) statistical methods. For the geographer or GIS analyst, however, spatial autocorrelation is evidence of important underlying spatial processes at work; it is an integral component of our data! Removing space removes data from their spatial context… it is like getting only half the story. The spatial processes and spatial relationships evident in our data, are a primary interest, and one of the reasons we get so excited about spatial data analysis. To avoid an over-counting type of bias in your model, however, you must identify the full set of explanatory variables that will effectively capture the inherent spatial structure in your dependent variable. If you cannot identify all of these variables, you will very likely see statistically significant spatial autocorrelation in the model residuals. Unfortunately, you cannot trust your regression results until this is remedied. Use the Spatial Autocorrelation tool to test for statistically significant spatial autocorrelation in your regression residuals.
There are at least three strategies for dealing with spatial autocorrelation in regression model residuals:
- Resample until the input variables no longer exhibit statistically significant spatial autocorrelation. While this does not insure the analysis is free of spatial autocorrelation problems, they are far less likely when spatial autocorrelation is removed from the dependent and explanatory variables. This is the traditional statistician's approach to dealing with spatial autocorrelation and is only appropriate if spatial autocorrelation is the result of data redundancy (the sampling scheme is too fine).
- Isolate the spatial and non-spatial components of each input variable using a spatial filtering regression method. Space is removed from each variable, but then it is put back into the regression model as a new variable to account for spatial effects/spatial structure. Spatial Filtering regression methods will be added to ArcGIS in a future release.
- Incorporate spatial autocorrelation into the regression model using spatial econometric regression methods. Econometric spatial regression methods will be added to ArcGIS in a future release.
There are at least 4 ways to deal with regional variation in OLS regression models:
- Include a variable in the model that explains the regional variation. If you see that your model is always over-predicting in the north and under-predicting in the south, for example, add a regional variable set to 1 for northern features and set to 0 for southern features.
- Use methods that incorporate regional variation into the regression model such as Geographically Weighted Regression (GWR).
- Consult robust regression standard errors and probabilities to determine if variable coefficients are statistically significant. See Interpreting OLS Regression Results. Geographically Weighted Regression is still recommended.
- Redefine/reduce the size of the study area so that the processes within it are all stationary - so they no longer exhibit regional variation.
Learn more about OLS regression
Learn more about GWR regression
Interpreting OLS Regression Results
Interpreting GWR Regression Results