Extensions > Spatial Analyst > Analysis concepts > Interpolation
Implementing Inverse Distance Weighted (IDW) |
|
|
Release 9.3
Last modified January 13, 2012 |
Print all topics in : "Interpolation" |
Note:
This topic was updated for 9.3.1.
Inverse Distance Weighted (IDW) is a method of interpolation that estimates cell values by averaging the values of sample data points in the neighborhood of each processing cell. The closer a point is to the center of the cell being estimated, the more influence, or weight, it has in the averaging process.
Learn how to calculate IDW using the Spatial Analyst toolbar
Learn how to calculate IDW interpolation using the IDW tool
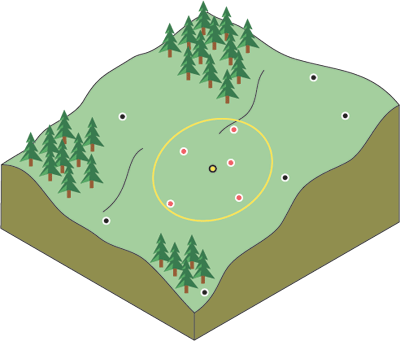
This method assumes that the variable being mapped decreases in influence with distance from its sampled location. For example, when interpolating a surface of consumer purchasing power for a retail site analysis, the purchasing power of a more distant location will have less influence because people are more likely to shop closer to home.
Power
With IDW you can control the significance of known points on the interpolated values based on their distance from the output point. By defining a higher power, more emphasis is placed on the nearest points, and the resulting surface will have more detail (be less smooth). Specifying a lower power will give more influence to the points that are farther away, resulting in a smoother surface. A power of two is most commonly used with IDW and is the default.
Search radius
The characteristics of the interpolated surface can be controlled by applying a fixed or variable search radius, which limits the number of input points that can be used for calculating each interpolated cell. You limit the number of points for each cell's calculation to improve processing speeds. You may also limit the number of points because points far from the cell location where the prediction is being made may have no spatial correlation.
Fixed search radius
A fixed search radius requires a neighborhood distance and a minimum number of points. The distance dictates the radius of the circle of the neighborhood (in map units). The distance of the radius is constant, so for each interpolated cell, the radius of the circle used to find input points is the same. The minimum number of points indicates the minimum number of measured points to use within the neighborhood. All the measured points that fall within the radius will be used in the calculation of each interpolated cell. When there are fewer measured points in the neighborhood than the specified minimum, the search radius will increase until it can encompass the minimum number of points. The specified fixed search radius will be used for each interpolated cell (cell center) in the study area; thus, if your measured points are not spread out equally (which they rarely are), there are likely to be a different number of measured points used in the different neighborhoods for the various predictions.
Variable search radius
With a variable search radius, the number of points used in calculating the value of the interpolated cell is specified, which makes the radius distance vary for each interpolated cell, depending on how far it has to search around each interpolated cell to reach the specified number of input points. Thus, some neighborhoods will be small and others will be large, depending on the density of the measured points near the interpolated cell. You can also specify a maximum distance (in map units) that the search radius cannot exceed. If the radius for a particular neighborhood reaches the maximum distance before obtaining the specified number of points, the prediction for that location will be performed on the number of measured points within the maximum distance. Generally, you will use smaller neighborhoods or a minimum number of points when the phenomenon has a great amount of variation.
Barrier
A barrier is a polyline dataset used as a breakline that limits the search for input sample points. A polyline can represent a cliff, ridge, or some other interruption in a landscape. Only those input sample points on the same side of the barrier as the current processing cell will be considered.