Geometry properties
Geometry properties
|
| Release 9.3 |
   |
There are many properties that characterize geometry. Some of these properties are described in this topic along with the functions you can use to determine the properties of a geometry.
You can use the following links to navigate to information about different geometry properties:
Dimensionality A geometry can have a dimension of 0, 1, or 2.
The dimensions are as follows:
- 0—Has neither length nor area
- 1—Has a length
- 2—Contains area
The point and multipoint subtypes have a dimension of 0. Points represent zero-dimensional features that can be modeled with a single coordinate, while multipoints represent data that must be modeled with a cluster of unconnected coordinates.
The subtypes linestring and multilinestring have a dimension of 1. They store features such as road segments, branching river systems, and any other features that are linear in nature.
Polygon and multipolygon subtypes have a dimension of 2. Forest stands, parcels, water bodies, and other features that have perimeters that enclose a definable area can be rendered by either the polygon or multipolygon data type.
Dimension is important not only as a property of the subtype but also in determining the spatial relationship of two features. The dimension of the resulting feature or features determines whether or not the operation was successful. The dimensions of the features are examined to determine how they should be compared.
To evaluate the dimension of a geometry, use the ST_Dimension function, which takes an ST_Geometry feature and returns its dimension as an integer. See ST_Dimension for syntax and an example of using this function.
The coordinates of a geometry also have dimensions. If a geometry has only x- and y-coordinates, the coordinate dimension is 2. If a geometry has x-, y-, and z-coordinates, the coordinate dimension is 3. If a geometry has x-, y-, z-, and m-coordinates, the coordinate dimension is 4. You can use the ST_CoordDim function to determine the dimensions present in a geometry.
Z-coordinates Some geometries have an associated altitude or depth—a third dimension. Each of the points that form the geometry of a feature can include an optional z-coordinate that represents an altitude or depth normal to the earth's surface.
The ST_Is3D predicate function takes an ST_Geometry and returns 1 (TRUE) if the function has z-coordinates and 0 (FALSE) if it does not.
You can determine a point's z-coordinate using the ST_Z function.
The ST_MaxZ function returns the maximum z-coordinate, and the function ST_MinZ returns the minimum z-coordinate of a geometry.
Measures Measures are values assigned to each coordinate. They are used for linear referencing and dynamic segmentation applications. For example, milepost locations along a highway can contain measures that indicate their position. The value represents anything that can be stored as a double-precision number.
The ST_IsMeasured predicate function takes a geometry and returns 1 (TRUE) if it contains measures and 0 (FALSE) if it does not (only used with the Oracle implementation of ST_Geometry).
You can discover a point's measure value by using the ST_M function.
Geometry typeAs mentioned in the topic The ST_Geometry storage type, ST_Geometry is a superclass that can store various subtypes. To determine what subtype a geometry is, use the ST_GeometryType or ST_Entity (Oracle only).
Point (vertex) collection and number of pointsA geometry can have zero or more points. A geometry is considered empty if it has zero points. The point subtype is the only geometry that is restricted to zero or one point; all other subtypes can have zero or more.
ST_PointAn ST_Point is a zero-dimensional geometry that occupies a single location in coordinate space. An ST_Point has a single x,y coordinate value, is always simple, and has a NULL boundary. ST_Point can be used to define features such as oil wells, landmarks, and water sample collection sites.
Functions that operate solely on the ST_Point data type include the following:
- ST_X—Returns a point data type's x-coordinate value as a double-precision number
- ST_Y—Returns a point data type's y-coordinate value as a double-precision number
- ST_Z—Returns a point data type's z-coordinate value as a double-precision number
- ST_M—Returns a point data type's m-coordinate value as a double-precision number
ST_MultiPointAn ST_MultiPoint is a collection of ST_Points and, like its elements, has a dimension of 0. An ST_MultiPoint is simple if none of its elements occupy the same coordinate space. The boundary of an ST_MultiPoint is NULL. ST_MultiPoints can define such things as aerial broadcast patterns and incidents of a disease outbreak.
Length and areaLength and area are measurable characteristics of geometries. Linestrings and the elements of multilinestrings are one-dimensional and possess the characteristic of length. Polygons and the elements of multipolygons are two-dimensional surfaces and, therefore, have an area you can measure. You can use the functions ST_Length and ST_Area to determine these properties. Units of measurement vary depending on how the data is stored.
ST_LineStringAn ST_LineString is a one-dimensional object stored as a sequence of points defining a linear interpolated path. The ST_LineString is simple if it does not intersect its interior. The endpoints (the boundary) of a closed ST_LineString occupy the same point in space. An ST_LineString is a ring if it is both closed and simple. Like the other properties inherited from the superclass ST_Geometry, ST_LineStrings have length. ST_LineStrings are often used to define linear features such as roads, rivers, and power lines.
The endpoints normally form the boundary of an ST_LineString unless the ST_LineString is closed, in which case the boundary is NULL. The interior of an ST_LineString is the connected path that lies between the endpoints unless it is closed, in which case the interior is continuous.
Functions that operate on ST_LineStrings include the following:
- ST_StartPoint—Returns the first point of the specified ST_LineString
- ST_EndPoint—Returns the last point of an ST_LineString
- ST_PointN—Takes an ST_LineString and an index to nth point and returns that point
- ST_Length—Returns the length of an ST_LineString as a double-precision number
- ST_NumPoints—Evaluates an ST_LineString and returns the number of points in its sequence as an integer
- ST_IsRing—A predicate function that returns 1 (TRUE) if the specified ST_LineString is a ring and 0 (FALSE) otherwise
- ST_IsClosed—A predicate function that returns 1 (TRUE) if the specified ST_LineString is closed and 0 (FALSE) if it is not
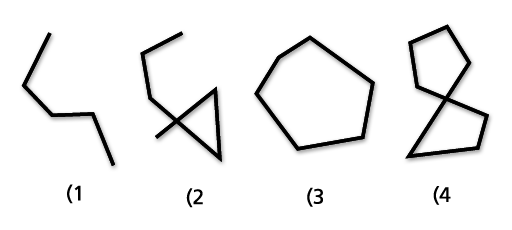
The graphic below shows examples of ST_LineString objects: (1) is a simple, nonclosed ST_LineString; (2) is a nonsimple, nonclosed ST_LineString; (3) is a closed, simple ST_LineString and, therefore, a ring; and (4) is a closed, nonsimple ST_LineString—it is not a ring.
 ST_MultiLineStringAn ST_MultiLineString is a collection of ST_LineStrings. ST_MultiLineStrings are simple if they only intersect at the endpoints of the ST_LineString elements. ST_MultiLineStrings are nonsimple if the interiors of the ST_LineString elements intersect.
The boundary of an ST_MultiLineString is the nonintersected endpoints of the ST_LineString elements. The ST_MultiLineString is closed if all of its ST_LineString elements are closed. The boundary of an ST_MultiLineString is NULL if all the endpoints of all the elements are intersected. In addition to the other properties inherited from the superclass ST_Geometry, ST_MultiLineStrings have length. ST_MultiLineStrings are used to define noncontiguous linear features, such as streams or road networks.
The following graphic provides examples of ST_MultiLineStrings: (1) is a simple ST_MultiLineString for which the boundary is the four endpoints of its two ST_LineString elements; (2) is a simple ST_MultiLineString because only the endpoints of the ST_LineString elements intersect. The boundary is two nonintersected endpoints; (3) is a nonsimple ST_MultiLineString, because the interior of one of its ST_LineString elements is intersected. The boundary of this ST_MultiLineString is the three nonintersected endpoints; (4) is a simple nonclosed ST_MultiLineString. It is not closed because its element ST_LineStrings are not closed. It is simple because none of the interiors of any of the element ST_LineStrings intersect; and (5) is a single, simple, closed ST_MultiLineString. It is closed because all of its elements are closed. It is simple because none of its elements intersect at the interiors.
ST_MultiLineStringAn ST_MultiLineString is a collection of ST_LineStrings. ST_MultiLineStrings are simple if they only intersect at the endpoints of the ST_LineString elements. ST_MultiLineStrings are nonsimple if the interiors of the ST_LineString elements intersect.
The boundary of an ST_MultiLineString is the nonintersected endpoints of the ST_LineString elements. The ST_MultiLineString is closed if all of its ST_LineString elements are closed. The boundary of an ST_MultiLineString is NULL if all the endpoints of all the elements are intersected. In addition to the other properties inherited from the superclass ST_Geometry, ST_MultiLineStrings have length. ST_MultiLineStrings are used to define noncontiguous linear features, such as streams or road networks.
The following graphic provides examples of ST_MultiLineStrings: (1) is a simple ST_MultiLineString for which the boundary is the four endpoints of its two ST_LineString elements; (2) is a simple ST_MultiLineString because only the endpoints of the ST_LineString elements intersect. The boundary is two nonintersected endpoints; (3) is a nonsimple ST_MultiLineString, because the interior of one of its ST_LineString elements is intersected. The boundary of this ST_MultiLineString is the three nonintersected endpoints; (4) is a simple nonclosed ST_MultiLineString. It is not closed because its element ST_LineStrings are not closed. It is simple because none of the interiors of any of the element ST_LineStrings intersect; and (5) is a single, simple, closed ST_MultiLineString. It is closed because all of its elements are closed. It is simple because none of its elements intersect at the interiors.
 Functions that operate on ST_MultiLineStrings include ST_Length and ST_IsClosed.
The ST_Length function evaluates an ST_MultiLineString and returns the cumulative length of all of its ST_LineString elements as a double-precision number.
The ST_IsClosed predicate function returns 1 (TRUE) if the specified ST_MultiLineString is closed and 0 (FALSE) if it is not closed.
ST_PolygonAn ST_Polygon is a two-dimensional surface stored as a sequence of points defining its exterior bounding ring and 0 or more interior rings. ST_Polygons are always simple. ST_Polygons define features that have spatial extent, such as parcels of land, water bodies, and areas of jurisdiction.
This graphic shows examples of ST_Polygon objects: (1) is an ST_Polygon for which the boundary is defined by an exterior ring; (2) is an ST_Polygon with a boundary defined by an exterior ring and two interior rings. The area inside the interior rings is part of the ST_Polygon's exterior; and (3) is a legal ST_Polygon, because the rings intersect at a single tangent point.
Functions that operate on ST_MultiLineStrings include ST_Length and ST_IsClosed.
The ST_Length function evaluates an ST_MultiLineString and returns the cumulative length of all of its ST_LineString elements as a double-precision number.
The ST_IsClosed predicate function returns 1 (TRUE) if the specified ST_MultiLineString is closed and 0 (FALSE) if it is not closed.
ST_PolygonAn ST_Polygon is a two-dimensional surface stored as a sequence of points defining its exterior bounding ring and 0 or more interior rings. ST_Polygons are always simple. ST_Polygons define features that have spatial extent, such as parcels of land, water bodies, and areas of jurisdiction.
This graphic shows examples of ST_Polygon objects: (1) is an ST_Polygon for which the boundary is defined by an exterior ring; (2) is an ST_Polygon with a boundary defined by an exterior ring and two interior rings. The area inside the interior rings is part of the ST_Polygon's exterior; and (3) is a legal ST_Polygon, because the rings intersect at a single tangent point.
 The exterior and any interior rings define the boundary of an ST_Polygon, and the space enclosed between the rings defines the ST_Polygon's interior. The rings of an ST_Polygon can intersect at a tangent point but never cross. In addition to the other properties inherited from the superclass ST_Geometry, ST_Polygons have area.
Functions that operate on an ST_Polygon include the following:
The exterior and any interior rings define the boundary of an ST_Polygon, and the space enclosed between the rings defines the ST_Polygon's interior. The rings of an ST_Polygon can intersect at a tangent point but never cross. In addition to the other properties inherited from the superclass ST_Geometry, ST_Polygons have area.
Functions that operate on an ST_Polygon include the following:
- ST_Area—Returns the area of an ST_Polygon as a double-precision number
- ST_Centroid—Returns an ST_Point that represents the center of the ST_Polygon's envelope
- ST_ExteriorRing—Returns the exterior ring of an ST_Polygon as an ST_LineString
- ST_InteriorRingN—Evaluates an ST_Polygon and an index and returns the nth interior ring as an ST_LineString
- ST_NumInteriorRing—Returns the number of interior rings that an ST_Polygon contains
- ST_PointOnSurface—Returns an ST_Point that is guaranteed to be on the surface of the specified ST_Polygon
ST_MultiPolygonThe boundary of an ST_MultiPolygon is the cumulative length of its elements' exterior and interior rings. The interior of an ST_MultiPolygon is defined as the cumulative interiors of its element ST_Polygons. The boundary of an ST_MultiPolygon's elements can only intersect at a tangent point. In addition to the other properties inherited from the superclass ST_Geometry, ST_MultiPolygons have area. ST_MultiPolygons define features such as a forest stratum or a noncontiguous parcel of land such as a Pacific island chain.
The graphic below provides examples of ST_MultiPolygon: (1) is ST_MultiPolygon with two ST_Polygon elements. The boundary is defined by the two exterior rings and the three interior rings; and (2) is an ST_MultiPolygon with two ST_Polygon elements. The boundary is defined by the two exterior rings and the two interior rings. The two ST_Polygon elements intersect at a tangent point. Functions that operate on ST_MultiPolygons include ST_Area, ST_Centroid, and ST_PointOnSurface.
The ST_Area function returns a double-precision number that represents the cumulative ST_Area of an ST_MultiPolygon's ST_Polygon elements.
The ST_Centroid function returns an ST_Point that is the center of an ST_MultiPolygon's envelope.
The ST_PointOnSurface function evaluates an ST_MultiPolygon and returns an ST_Point that is guaranteed to be normal to the surface of one of its ST_Polygon elements.
Number of simple geometries in a multipart geometryMultipart geometries are made up of individual geometries. You might want to determine how many individual geometries are in a multipart geometry, such as an ST_MultiPoint, ST_MultiLineString, and ST_MultiPolygon. To do this, use the ST_NumGeometries predicate function. This function returns a count of the individual elements in a collection of geometries.
Using the ST_GeometryN function, you can determine which geometry in the multipart geometry exists in position N, N being a number you provide with the function. For example, if you want to return the third point of a multipoint geometry, you would include 3 when you execute the function.
Interior, boundary, exterior All geometries occupy a position in space defined by their interiors, boundaries, and exteriors. The exterior of a geometry is all the space not occupied by the geometry. The interior is the space occupied by the geometry. The boundary of a geometry is the location between its interior and exterior. The subtype inherits the interior and exterior properties directly; however, the boundary property differs for each.
Use the ST_Boundary function to determine the source ST_Geometry's boundary. See ST_Boundary for syntax and an example.
Simple or nonsimple Some subtypes of ST_Geometry are always simple such as ST_Points or ST_Polygons. However, the subtypes ST_LineStrings, ST_MultiPoints, and ST_MultiLineStrings can be either simple or nonsimple. They are simple if they obey all topological rules imposed on them and nonsimple if they do not.
Some topological rules include the following:
Functions that operate on ST_MultiPolygons include ST_Area, ST_Centroid, and ST_PointOnSurface.
The ST_Area function returns a double-precision number that represents the cumulative ST_Area of an ST_MultiPolygon's ST_Polygon elements.
The ST_Centroid function returns an ST_Point that is the center of an ST_MultiPolygon's envelope.
The ST_PointOnSurface function evaluates an ST_MultiPolygon and returns an ST_Point that is guaranteed to be normal to the surface of one of its ST_Polygon elements.
Number of simple geometries in a multipart geometryMultipart geometries are made up of individual geometries. You might want to determine how many individual geometries are in a multipart geometry, such as an ST_MultiPoint, ST_MultiLineString, and ST_MultiPolygon. To do this, use the ST_NumGeometries predicate function. This function returns a count of the individual elements in a collection of geometries.
Using the ST_GeometryN function, you can determine which geometry in the multipart geometry exists in position N, N being a number you provide with the function. For example, if you want to return the third point of a multipoint geometry, you would include 3 when you execute the function.
Interior, boundary, exterior All geometries occupy a position in space defined by their interiors, boundaries, and exteriors. The exterior of a geometry is all the space not occupied by the geometry. The interior is the space occupied by the geometry. The boundary of a geometry is the location between its interior and exterior. The subtype inherits the interior and exterior properties directly; however, the boundary property differs for each.
Use the ST_Boundary function to determine the source ST_Geometry's boundary. See ST_Boundary for syntax and an example.
Simple or nonsimple Some subtypes of ST_Geometry are always simple such as ST_Points or ST_Polygons. However, the subtypes ST_LineStrings, ST_MultiPoints, and ST_MultiLineStrings can be either simple or nonsimple. They are simple if they obey all topological rules imposed on them and nonsimple if they do not.
Some topological rules include the following:
- An ST_LineString is simple if it does not intersect its interior and nonsimple if it does.
- An ST_MultiPoint is simple if none of its elements occupies the same coordinate space (have the same x,y coordinates) and nonsimple if they do.
- An ST_MultiLineString is simple if none of its elements' interiors is intersected by its own interior and nonsimple if the elements' interiors do intersect.
The ST_IsSimple predicate function is used to determine if an ST_LineString, ST_MultiPoint, or ST_MultiLineString is simple or nonsimple. ST_IsSimple takes an ST_Geometry and returns 1 (TRUE) if the ST_Geometry is simple and 0 (FALSE) if it is not. See ST_IsSimple for syntax and an example of using this function.
Empty or not empty A geometry is empty if it does not have any points. An empty geometry has a NULL envelope, boundary, interior, and exterior. An empty geometry is always simple. Empty linestrings and multilinestrings have a 0 length. Empty polygons and multipolygons have a 0 area.
The ST_IsEmpty predicate function can be used to determine if a geometry is empty. It analyzes an ST_Geometry and returns 1 (TRUE) if the ST_Geometry is empty and 0 (FALSE) if it is not. See ST_IsEmpty for syntax and an example of using this function.
IsClosed and IsRingLinestring geometries can be closed and/or be rings. Linestrings can be closed without being rings. You can determine if a linestring is closed by using the ST_IsClosed predicate function; it returns TRUE if the start point and endpoint of the linestring intersect. Rings are linestrings that are closed and simple. The ST_IsRing predicate function can be used to test if a linestring is truly a ring; it returns TRUE if the linestring is closed and is simple.
See ST_IsClosed and ST_IsRing for syntax and examples.
Envelope Every geometry has an envelope. The envelope of a geometry is the bounding geometry formed by the minimum and maximum x,y coordinates. For point geometries, since the minimum and maximum x,y coordinates are the same, a rectangle is created around these coordinates to create an envelope. For line geometries, the line's endpoints represent two sides of the envelope and the other two sides are created just above and just below the line.
The ST_Envelope function takes an ST_Geometry and returns an ST_Geometry that represents the source ST_Geometry's envelope. See ST_Envelope for syntax and an example.
To find the individual minimum and maximum x,y coordinates of a geometry, use the functions ST_MinX, ST_MinY, ST_MaxX, and ST_MaxY.
Spatial reference system The spatial reference system identifies the coordinate transformation matrix for each geometry. All spatial reference systems known to the database are stored in the spatial_references table.
There are two functions used to get information about spatial reference systems of geometries: ST_SRID and ST_EqualSRS.
The ST_SRID function takes an ST_Geometry and returns its spatial reference identifier as an integer.
The ST_EqualSRS function determines if the spatial reference systems of two different feature classes are identical or not.
For syntax and examples of these functions, see ST_SRID and ST_EqualSRS.
You can find more information on spatial references in the topic The properties of a spatial reference. When using an IBM DBMS, see the IBM DB2 Spatial Extender and Geodetic Extender User's Guide and Reference or the IBM Informix Spatial DataBlade Module User's Guide.
Size of features (PostgreSQL only)The features (spatial records in a table) take up a certain amount of storage space in bytes. You can use the ST_GeoSize function to determine how big each feature in a table is.


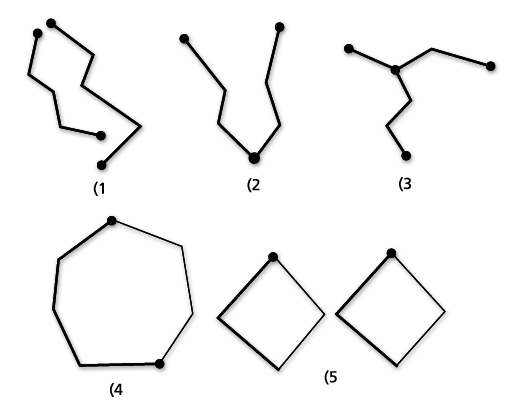
 ST_MultiLineStringAn ST_MultiLineString is a collection of ST_LineStrings. ST_MultiLineStrings are simple if they only intersect at the endpoints of the ST_LineString elements. ST_MultiLineStrings are nonsimple if the interiors of the ST_LineString elements intersect.
The boundary of an ST_MultiLineString is the nonintersected endpoints of the ST_LineString elements. The ST_MultiLineString is closed if all of its ST_LineString elements are closed. The boundary of an ST_MultiLineString is NULL if all the endpoints of all the elements are intersected. In addition to the other properties inherited from the superclass ST_Geometry, ST_MultiLineStrings have length. ST_MultiLineStrings are used to define noncontiguous linear features, such as streams or road networks.
The following graphic provides examples of ST_MultiLineStrings: (1) is a simple ST_MultiLineString for which the boundary is the four endpoints of its two ST_LineString elements; (2) is a simple ST_MultiLineString because only the endpoints of the ST_LineString elements intersect. The boundary is two nonintersected endpoints; (3) is a nonsimple ST_MultiLineString, because the interior of one of its ST_LineString elements is intersected. The boundary of this ST_MultiLineString is the three nonintersected endpoints; (4) is a simple nonclosed ST_MultiLineString. It is not closed because its element ST_LineStrings are not closed. It is simple because none of the interiors of any of the element ST_LineStrings intersect; and (5) is a single, simple, closed ST_MultiLineString. It is closed because all of its elements are closed. It is simple because none of its elements intersect at the interiors.
ST_MultiLineStringAn ST_MultiLineString is a collection of ST_LineStrings. ST_MultiLineStrings are simple if they only intersect at the endpoints of the ST_LineString elements. ST_MultiLineStrings are nonsimple if the interiors of the ST_LineString elements intersect.
The boundary of an ST_MultiLineString is the nonintersected endpoints of the ST_LineString elements. The ST_MultiLineString is closed if all of its ST_LineString elements are closed. The boundary of an ST_MultiLineString is NULL if all the endpoints of all the elements are intersected. In addition to the other properties inherited from the superclass ST_Geometry, ST_MultiLineStrings have length. ST_MultiLineStrings are used to define noncontiguous linear features, such as streams or road networks.
The following graphic provides examples of ST_MultiLineStrings: (1) is a simple ST_MultiLineString for which the boundary is the four endpoints of its two ST_LineString elements; (2) is a simple ST_MultiLineString because only the endpoints of the ST_LineString elements intersect. The boundary is two nonintersected endpoints; (3) is a nonsimple ST_MultiLineString, because the interior of one of its ST_LineString elements is intersected. The boundary of this ST_MultiLineString is the three nonintersected endpoints; (4) is a simple nonclosed ST_MultiLineString. It is not closed because its element ST_LineStrings are not closed. It is simple because none of the interiors of any of the element ST_LineStrings intersect; and (5) is a single, simple, closed ST_MultiLineString. It is closed because all of its elements are closed. It is simple because none of its elements intersect at the interiors.
 Functions that operate on ST_MultiLineStrings include ST_Length and ST_IsClosed.
The ST_Length function evaluates an ST_MultiLineString and returns the cumulative length of all of its ST_LineString elements as a double-precision number.
The ST_IsClosed predicate function returns 1 (TRUE) if the specified ST_MultiLineString is closed and 0 (FALSE) if it is not closed.
ST_PolygonAn ST_Polygon is a two-dimensional surface stored as a sequence of points defining its exterior bounding ring and 0 or more interior rings. ST_Polygons are always simple. ST_Polygons define features that have spatial extent, such as parcels of land, water bodies, and areas of jurisdiction.
This graphic shows examples of ST_Polygon objects: (1) is an ST_Polygon for which the boundary is defined by an exterior ring; (2) is an ST_Polygon with a boundary defined by an exterior ring and two interior rings. The area inside the interior rings is part of the ST_Polygon's exterior; and (3) is a legal ST_Polygon, because the rings intersect at a single tangent point.
Functions that operate on ST_MultiLineStrings include ST_Length and ST_IsClosed.
The ST_Length function evaluates an ST_MultiLineString and returns the cumulative length of all of its ST_LineString elements as a double-precision number.
The ST_IsClosed predicate function returns 1 (TRUE) if the specified ST_MultiLineString is closed and 0 (FALSE) if it is not closed.
ST_PolygonAn ST_Polygon is a two-dimensional surface stored as a sequence of points defining its exterior bounding ring and 0 or more interior rings. ST_Polygons are always simple. ST_Polygons define features that have spatial extent, such as parcels of land, water bodies, and areas of jurisdiction.
This graphic shows examples of ST_Polygon objects: (1) is an ST_Polygon for which the boundary is defined by an exterior ring; (2) is an ST_Polygon with a boundary defined by an exterior ring and two interior rings. The area inside the interior rings is part of the ST_Polygon's exterior; and (3) is a legal ST_Polygon, because the rings intersect at a single tangent point.
 The exterior and any interior rings define the boundary of an ST_Polygon, and the space enclosed between the rings defines the ST_Polygon's interior. The rings of an ST_Polygon can intersect at a tangent point but never cross. In addition to the other properties inherited from the superclass ST_Geometry, ST_Polygons have area.
Functions that operate on an ST_Polygon include the following:
The exterior and any interior rings define the boundary of an ST_Polygon, and the space enclosed between the rings defines the ST_Polygon's interior. The rings of an ST_Polygon can intersect at a tangent point but never cross. In addition to the other properties inherited from the superclass ST_Geometry, ST_Polygons have area.
Functions that operate on an ST_Polygon include the following:
 Functions that operate on ST_MultiPolygons include ST_Area, ST_Centroid, and ST_PointOnSurface.
The ST_Area function returns a double-precision number that represents the cumulative ST_Area of an ST_MultiPolygon's ST_Polygon elements.
The ST_Centroid function returns an ST_Point that is the center of an ST_MultiPolygon's envelope.
The ST_PointOnSurface function evaluates an ST_MultiPolygon and returns an ST_Point that is guaranteed to be normal to the surface of one of its ST_Polygon elements.
Number of simple geometries in a multipart geometryMultipart geometries are made up of individual geometries. You might want to determine how many individual geometries are in a multipart geometry, such as an ST_MultiPoint, ST_MultiLineString, and ST_MultiPolygon. To do this, use the ST_NumGeometries predicate function. This function returns a count of the individual elements in a collection of geometries.
Using the ST_GeometryN function, you can determine which geometry in the multipart geometry exists in position N, N being a number you provide with the function. For example, if you want to return the third point of a multipoint geometry, you would include 3 when you execute the function.
Interior, boundary, exterior All geometries occupy a position in space defined by their interiors, boundaries, and exteriors. The exterior of a geometry is all the space not occupied by the geometry. The interior is the space occupied by the geometry. The boundary of a geometry is the location between its interior and exterior. The subtype inherits the interior and exterior properties directly; however, the boundary property differs for each.
Use the ST_Boundary function to determine the source ST_Geometry's boundary. See ST_Boundary for syntax and an example.
Simple or nonsimple Some subtypes of ST_Geometry are always simple such as ST_Points or ST_Polygons. However, the subtypes ST_LineStrings, ST_MultiPoints, and ST_MultiLineStrings can be either simple or nonsimple. They are simple if they obey all topological rules imposed on them and nonsimple if they do not.
Some topological rules include the following:
Functions that operate on ST_MultiPolygons include ST_Area, ST_Centroid, and ST_PointOnSurface.
The ST_Area function returns a double-precision number that represents the cumulative ST_Area of an ST_MultiPolygon's ST_Polygon elements.
The ST_Centroid function returns an ST_Point that is the center of an ST_MultiPolygon's envelope.
The ST_PointOnSurface function evaluates an ST_MultiPolygon and returns an ST_Point that is guaranteed to be normal to the surface of one of its ST_Polygon elements.
Number of simple geometries in a multipart geometryMultipart geometries are made up of individual geometries. You might want to determine how many individual geometries are in a multipart geometry, such as an ST_MultiPoint, ST_MultiLineString, and ST_MultiPolygon. To do this, use the ST_NumGeometries predicate function. This function returns a count of the individual elements in a collection of geometries.
Using the ST_GeometryN function, you can determine which geometry in the multipart geometry exists in position N, N being a number you provide with the function. For example, if you want to return the third point of a multipoint geometry, you would include 3 when you execute the function.
Interior, boundary, exterior All geometries occupy a position in space defined by their interiors, boundaries, and exteriors. The exterior of a geometry is all the space not occupied by the geometry. The interior is the space occupied by the geometry. The boundary of a geometry is the location between its interior and exterior. The subtype inherits the interior and exterior properties directly; however, the boundary property differs for each.
Use the ST_Boundary function to determine the source ST_Geometry's boundary. See ST_Boundary for syntax and an example.
Simple or nonsimple Some subtypes of ST_Geometry are always simple such as ST_Points or ST_Polygons. However, the subtypes ST_LineStrings, ST_MultiPoints, and ST_MultiLineStrings can be either simple or nonsimple. They are simple if they obey all topological rules imposed on them and nonsimple if they do not.
Some topological rules include the following: